646

What Do You Understand About Partial Fractions?

Many complex rational expressions can be found in mathematics. We will take a lot longer to find the solution if we attempt to solve problems in a complicated way. By taking the complex expression and reducing it to the simpler one, we avoid this complexity. In partial fractions, polynomials are “broken apart” into smaller fractions. In partial fraction decomposition, rational expressions are broken down into simpler partial fractions. Integration is more effective with this process. Here’s a comprehensive article that explains partial fractions, decomposition of partial fractions, and partial fractions in an improper fraction with solved examples.

Definition of Partial Fraction 

It is possible to break down algebraic fractions into simpler parts, called “partial fractions”. 

Let us explain by taking this example of the algebraic fraction which is 

 (3x+5)/ (2x2-5x-3). You can break this expression into simpler parts like (2)/(x-3) – (1)/ (2x+1).

These simpler parts like [(2)/(x-3)]-[(1)/ (2x+1)] are the partial fractions.

Therefore, the algebraic expression may be written in the form shown in figure 1. This means that the algebraic expression can be written in the form given in the figure:

 

 

 

 

 

 

 

 

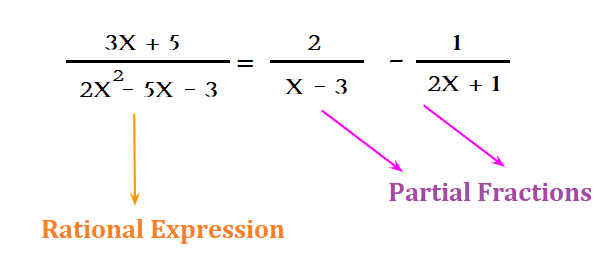
Notice: Decomposition of fractions using partial fractions only works for rational expressions. Rational are those where the degree of the numerator is lesser as compared to the degree of the denominator. If the rational expression has improper fraction expression where the numerator would be greater when compared to the denominator, then divide numbers to convert them into rational expressions properly. Use the polynomial long division method, you can achieve this.

Partial Fraction Formula

Detailed steps are given here for calculating partial fraction decomposition based on the formula:

Step 1: Starting with the correct rational expression, decompose the rational expression into the partial fraction.

Step 2: Now, you are required to convert into a linear factor, the factored denominator present in the rational expression. But, remember here not to factor this denominator into a complex number.  

Step 3: Now, write the partial fractions for each variable obtained, e.g., A and B in the numerators.

Step 4: Multiply the whole equation by the denominator to find A and B’s values.

Step 5: Substitute zero in the factor variable to solve for the variables.

Step 6: Use the partial fraction values for A and B.

How to Calculate Partial Fractions from Rational Functions?

Rational numbers are those which can easily be expressed in terms of p/q, meaning q is a single integer and p is an integer. Also, remember here, q should not be equal to 0. In the same way, a rational function can be defined as a ratio of two polynomial functions like P(x), Q(x), where P and Q both are polynomials in x and Q(x) is not equal to 0. Proper rational functions have P(x) less than Q(x); improper rational functions do not. The rational functions can be converted to proper ones using the long division process. If P(x)/Q(x) are improper, then they could be written as:

[Latex]\frac {P(x)} {Q(x)} = A(x) + \frac{R(x)} {Q(x)} [/latex]

Here, A (x) represents a polynomial in x, while R(x)/Q(x) represents a proper rational function.

Integrating a function f(x) gives us F(x) and the integration is demonstrated by:

∫f(x) dx = F(x) + C

C is the constant of integration and R.H.S. stands for integral of f(x) in relation to x.

What is Partial Fractions Decomposition?

Integration of a rational function is accomplished by reducing it to a rational function. Decomposition into partial fractions entails the summation of simple rational functions to represent the integrand. Traditional integrating techniques are used to integrate the integrand accordingly after splitting it into partial fractions.

What is Partial Fraction of Improper Fraction?

The numerator of an algebraic fraction must be greater than or equal to the denominator to be valid. Polynomials have degrees that are the highest powers. Consider a denominator and a numerator with degrees m and n, respectively. Furthermore, in addition to the partial fractions due to the factors in the denominator, an additional term must be included: this extra term is a polynomial of degree n − m.

Note: 

• Whenever K is a constant, then K is a polynomial with zero degree
• Px + Q are polynomials of degree 1
• Px2+Qx+K is a polynomial of degree 2

 

Conclusion

Here we have tried to explain to you in brief about partial fractions, improper fractions and how to solve them. As we all know maths is about practice, thus, you must go to the Cuemath website and solve the practice questions on partial fractions there.